Unit 4: Motion in Two and Three Dimensions

Position and Displacement

One general way of locating a particle (or particle-like object) is with a position vector r⃗\vec r, which is a vector that extends from a reference point (usually the origin) to the particle. In the unit-vector notation:

r⃗=xi^+yj^+zk^\vec r = x\hat i + y\hat j + z\hat k

where xi^x\hat i, yj^y\hat j, and zk^z\hat k are the vector components of r⃗\vec r and the coefficients xx, yy, and zz are its scalar components.

As a particle moves, its position vector changes in such a way that the vector always extends to the particle from the reference point (the origin). If the position vector changes—say, from r⃗1\vec r_1 to r⃗2\vec r_2 during a certain time interval—then the particle’s displacement Δr⃗\Delta \vec r during that time interval is

Δr⃗=r⃗2−r⃗1 \Delta \vec r = \vec r_2 - \vec r_1

This can be rewritten using unit vector notation as follows:

Δr⃗=(x2−x1)i^+(y2−y1)j^+(z2−z1)k^\Delta \vec r = (x_2 - x_1)\hat i + (y_2 - y_1)\hat j + (z_2 - z_1)\hat k

or more simply

Δr⃗=Δxi^+Δyj^+Δzk^\Delta \vec r = \Delta x \hat i + \Delta y \hat j + \Delta z \hat k

Average and Instantaneous Velocity

If a particle moves through a displacement Δr⃗\Delta \vec r in a time interval Δt\Delta t, then its average velocity v⃗avg\vec v_{avg} is

v⃗avg=Δr⃗Δt\vec v_{avg} = \frac{\Delta \vec r}{\Delta t}

The direction of v⃗avg\vec v_{avg} must be the same as that of the displacement Δr⃗\Delta \vec r. This formula can also be written in components:

v⃗avg=ΔxΔti^+ΔyΔtj^+ΔzΔtk^\vec v_{avg} = \frac{\Delta x}{\Delta t}\hat i + \frac{\Delta y}{\Delta t}\hat j + \frac{\Delta z}{\Delta t}\hat k

When we speak of the velocity of a particle, we usually mean the particle’s instantaneous velocity v⃗\vec v at some instant. This v⃗\vec v is the value that v⃗avg\vec v_{avg} approaches in the limit as we shrink the time interval Δt\Delta t to 0 about that instant. Using the language of calculus, we may write v⃗\vec v as the derivative.

v⃗=dr⃗dt\vec v = \frac{d \vec r}{dt}

Average Acceleration and Instantaneous Acceleration

When a particle’s velocity changes from v⃗1\vec v_1 to v⃗2\vec v_2 in a time interval Δt\Delta t, its average acceleration a⃗vg\vec a_{vg} during Δt\Delta t is:

a⃗avg=Δv⃗Δt\vec a_{avg} = \frac{\Delta \vec v}{\Delta t}

If we shrink Δt\Delta t to zero about some instant, then in the limit a⃗avg\vec a_{avg} approaches the instantaneous acceleration (or acceleration) a⃗\vec a at that instant; that is,

a⃗=dv⃗dt\vec a = \frac{d \vec v}{dt}

If the velocity changes in either magnitude or direction (or both), the particle must have an acceleration.

This equation can also be written in vector form as

a⃗=dv⃗xdti^+dv⃗ydtj^+dv⃗zdtk^\vec a = \frac{d\vec v_x}{dt}\hat i + \frac{d\vec v_y}{dt}\hat j + \frac{d\vec v_z}{dt}\hat k

The scalar components of a⃗\vec a can be found by differentiating the scalar components of v⃗\vec v.

Particle Motion

Uniform Circular Motion

Relative Motion

The velocity of a particle depends on the reference frame of whoever is observing or measuring the velocity. For our purposes, a reference frame is the physical object to which we attach our coordinate system. In everyday life, that object is the ground. For example, the speed listed on a speeding ticket is always measured relative to the ground. The speed relative to the police officer would be different if the officer were moving while making the speed measurement.

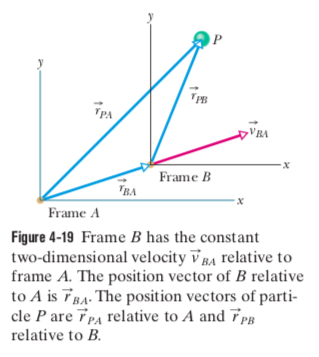
When two frames of reference A and B are moving relative to each other at constant velocity, the velocity of a particle P as measured by an observer in frame A usually differs from that measured from frame B. The two measured velocities are related by:

v⃗PA=v⃗PB+v⃗BA\vec v_{PA} = \vec v_{PB} + \vec v_{BA}

Where v⃗BA\vec v_{BA} is the velocity of BB with respect to AA. Both observers measure the same acceleration for the particle:

a⃗PA=a⃗PB\vec a_{PA} = \vec a_{PB}

Two Dimensions

In this scenario, the head-to tail vectors can be arranged to get the following formula:

r⃗PA=r⃗PB+r⃗BA\vec r_{PA} = \vec r_{PB} + \vec r_{BA}

Taking the time derivative gives a similar formula for velocity:

v⃗PA=v⃗PB+v⃗BA\vec v_{PA} = \vec v_{PB} + \vec v_{BA}

And the following equation for acceleration:

a⃗PA=a⃗PB\vec a_{PA} = \vec a_{PB}

As for one-dimensional motion, we have the following rule: Observers on different frames of reference that move at constant velocity relative to each other will measure the same acceleration for a moving particle.