Unit 30: Induction and Inductance

30.1 - Faraday’s Law and Lenz’s Law

Faraday’s Law of Induction

Faraday's law of induction describes how an electric current produces a magnetic field and, conversely, how a changing magnetic field generates an electric current in a conductor.

Magnetic Flux

To put Faraday’s law to work, we need a way to calculate the amount of magnetic field that passes through a loop. Suppose a loop enclosing an area $A$ is placed in a magnetic field $\vec B$ . Then the magnetic flux through the loop is:

\Phi_B = \int \vec B \cdot dA

💡

As with electric flux, we want the component of the field that pierces the surface (not skims along it).

Uniform, Parallel Magnetic Field

Suppose that the loop lies in a plane and that the magnetic field is perpendicular to the plane of the loop. This simplifies the above equation to:

\Phi_B = BA \hspace{2em} (\vec B \perp \textrm{area}, \vec B \textrm{ uniform})

Magnetic flux is measured in Webers:

1 \space \textrm{weber} = 1 \space \textrm{Wb} = 1 \space \textrm T \cdot \textrm m^2

Faraday’s Law

The magnitude of the emf $\mathscr E$ induced in a conducting loop is equal to the rate at which the magnetic flux $\vec B$ through that loop changes with time.

\mathscr E = -\frac{d\Phi_B}{dt}

If we change the magnetic flux through a coil of $N$ turns, an induced emf appears in every turn and the total emf induced in the coil is the sum of these individual induced emfs. If the coil is tightly wound (closely packed), so that the same magnetic flux $\Phi_B$ passes through all the turns, the total emf induced in the coil is:

\mathscr E = -N \frac{d\Phi_B}{dt} \hspace{2em} (\textrm{coil of } N \textrm{ turns})

Lenz’s Law

Soon after Faraday proposed his law of induction, Heinrich Friedrich Lenz devised a rule for determining the direction of an induced current in a loop:

⭐

An induced current has a direction such that the magnetic field due to the current opposes the change in the magnetic flux that induces the current.

30.2 - Induction and Energy Transfers

The induction of a current by a changing flux means that energy is being transferred to that current. The energy can then be transferred to other forms, such as thermal energy.

Eddy Currents

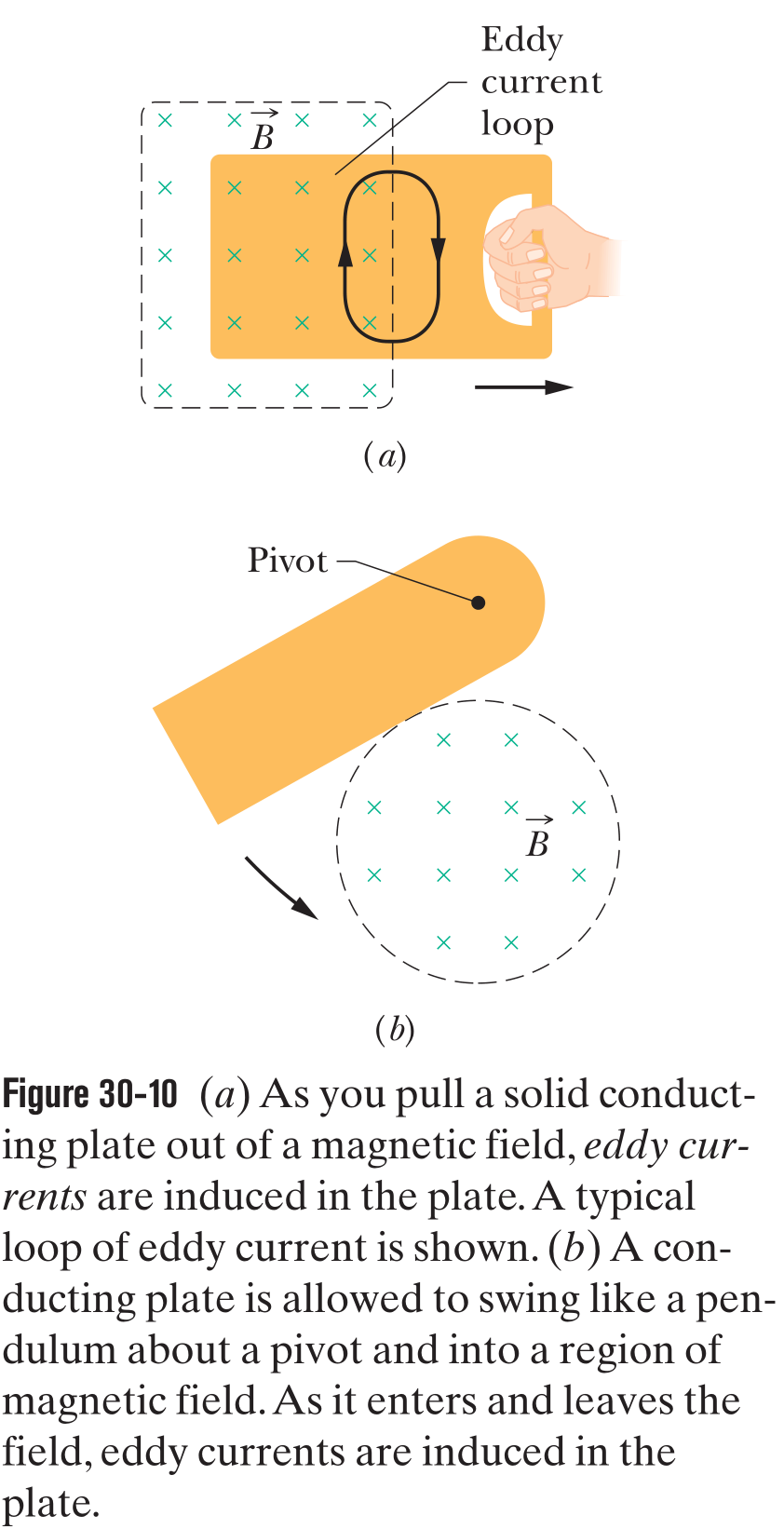
Suppose we move a solid conducting plate out of a magnetic field, as shown above. The relative motion of the field and the conductor again induces a current in the conductor. Thus, we again encounter an opposing force and must do work because of the induced current. With the plate, however, the conduction electrons making up the induced current do not follow one path as they do with the loop. Instead, the electrons swirl about within the plate as if they were caught in an eddy (whirlpool) of water. Such a current is called an eddy current, and can be represented as if it followed a single path as shown above.

30.3 - Induced Electric Fields

An emf is induced by a changing magnetic flux even if the loop through which the flux is changing is not a physical conductor but an imaginary line. The changing magnetic field induces an electric field $\vec E$ at every point of such a loop; the induced emf is related to $\vec E$ by:

\mathscr{E} = \oint \vec E \cdot d\vec s

Using the induced electric field, we can write Faraday’s law in its most general form as:

\oint \vec E \cdot d\vec s = -\frac{d\Phi_b}{dt}

30.4 - Inductors and Inductance

An inductor is a device (coil, toroid, or solenoid) that can be used to produce a known magnetic field in a specified region. If a current $i$ is established through each of the $N$ windings of an inductor, a magnetic flux $\Phi_B$ links those windings. The inductance $L$ of the inductor is:

L = \frac{N\Phi_B}{i}

The SI unit of inductance is the henry (H), where:

1 \space \textrm{henry} = 1 \space \textrm{H} = 1 \space \textrm{T} \cdot \textrm m ^2 / \textrm A

The inductance per unit length near the middle of a long solenoid of cross-sectional area $A$ and $n$ turns per unit length is:

\frac{L}{l} = \mu_0n^2A

30.5 - Self-Induction

If a current $i$ in a coil changes with time, an emf is induced in the coil. This self-induced emf is:

\mathscr E_L = -L\frac{di}{dt}

The direction of $\mathscr E_L$ is found from Lenz’s law: The self-induced emf acts to oppose the charge that produces it.

30.6 - RL Circuits

If a constant emf $\mathscr E$ is introduced into a single-loop circuit containing a resistance $R$ and an inductance $L$ , the current rises to an equilibrium value of $\mathscr E / R$ according to:

i = \frac{\mathscr E}{R}(1-e^{-t/\tau_L})

Here $\tau_L (=L/R)$ governs the rate of rise of the current and is called the inductive time constant of the circuit.

When the course of constant emf is removed, the current decays from a value $i_0$ according to:

i = i_0 e^{-t/\tau_L}

30.7 - Energy Stored in a Magnetic Field

If an inductor $L$ carries a current $i$ , the inductor’s magnetic field stores an energy given by:

U_B = \frac{1}{2} Li^2

30.8 - Energy Density of a Magnetic Field

If $B$ is the magnitude of a magnetic field at any point (in an inductor or anywhere else), the density of stored magnetic energy at that point is:

u_B = \frac{B^2}{2\mu_0}

30.9 - Mutual Induction

If coils 1 and 2 are near each other, a changing current in either coil can induce an emf in the other. This mutual induction is described by:

\mathscr E_2 = -M \frac{di_1}{dt}

\mathscr E_1 = -M \frac{di_2'}{dt}

where $M$ (measured in henries) is the mutual inductance.