29.1 - Magnetic Field Due to a Current

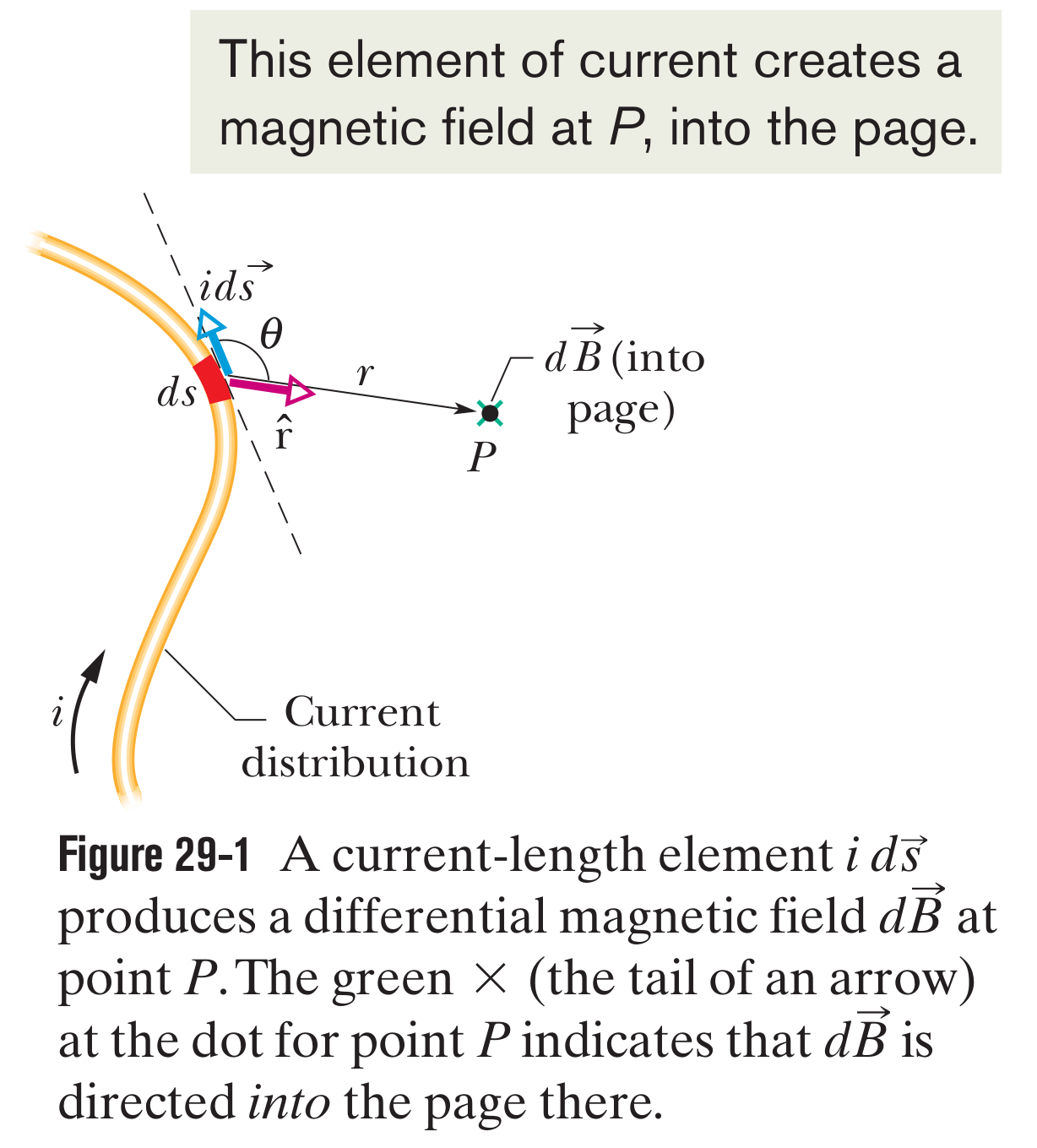
The magnetic field set up by a current-carrying conductor can be found from the Biot-Savart law. This law asserts that the contribution $d\vec B$ to the field produced by a current-length element $i \space d\vec s$ at a point $P$ located a distance $r$ from the current element is:

Here, $\hat r$ is a unit vector that points from the element towards $P$. The quantity $\mu_0$, called the permeability constant, has the value:

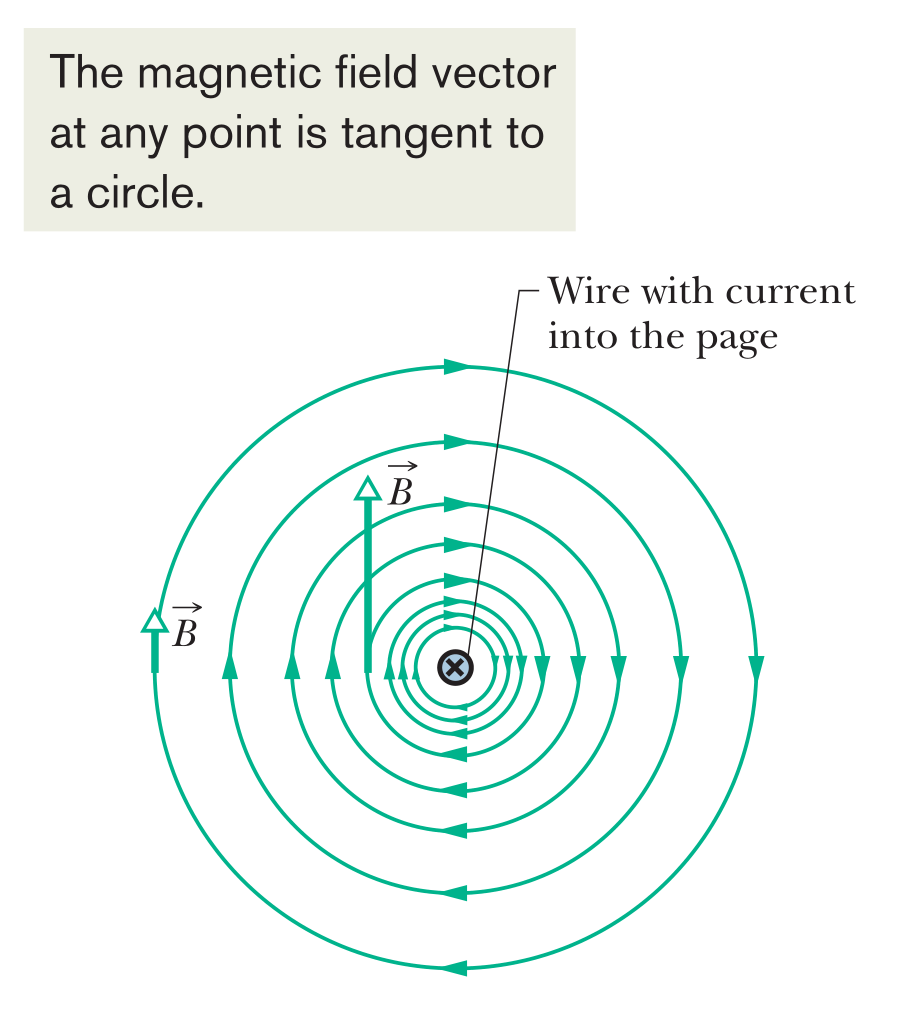
Long Straight Wire

For a long straight wire carrying current $i$, the Biot-Savart law gives, for the magnitude of the magnetic field at a perpendicular distance $R$ from the wire:

$$B = \frac{\mu_0 i}{2\pi R} \hspace{1em} \textrm{(long straight wire)}$$

Circular Arc of Wire

The magnitude of the magnetic field at the center of a circular arc, of radius $R$ and central angle $\phi$ (in radians), carrying current $i$, is:

29.2 - Force Between Two Parallel Currents

Parallel wires carrying currents in the same direction attract each other, whereas parallel wires carrying currents in opposite directions repel each other. The magnitude of the force on a length $L$ of either wire is:

where $d$ is the wire separation, and $i_a$ and $i_b$ are the currents in the wires.

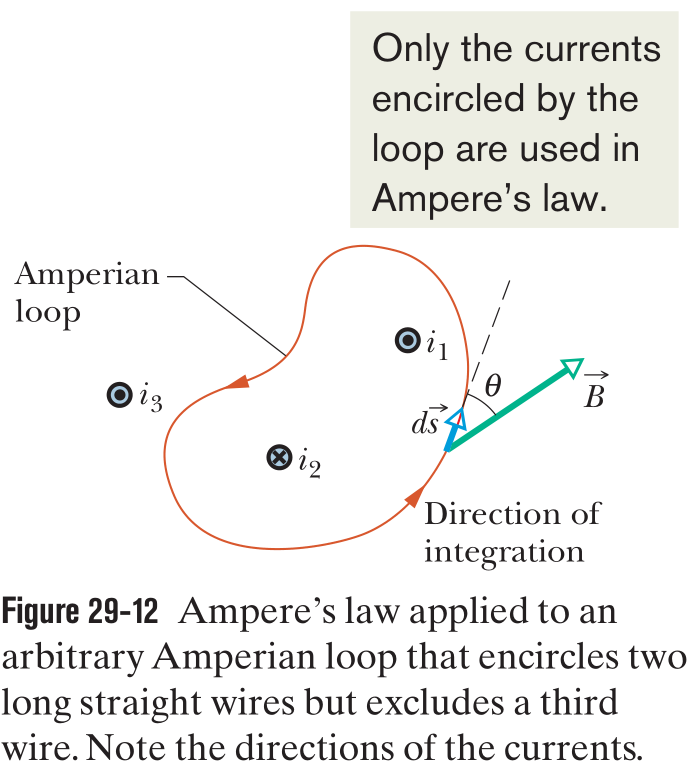
29.3 - Ampere’s Law

Ampere’s Law states that:

$$\oint \vec B \cdot d\vec s = \mu_0 i_{enc}$$

The line integral in this equation is evaluated around a closed loop called an Amperian loop. The current $i$ on the right side is the net current encircled by the loop.

29.4 - Solenoids and Toroids

Solenoids

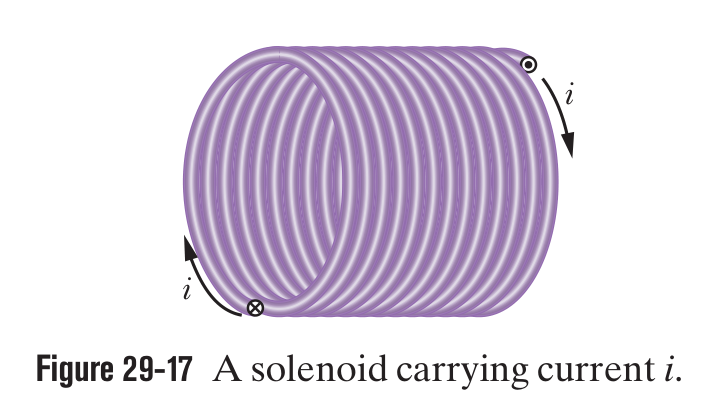
A solenoid is a long, tightly wound helical coil of wire, in which the length is far greater than the diameter. The magnetic field produced within the solenoid is the vector sum of the fields produced by the individual turns (windings) that make up the solenoid.

Inside a long solenoid carrying current $i$, at points not near its ends, the magnitude $B$ of the magnetic field is:

where $n$ is the number of turns per unit length.

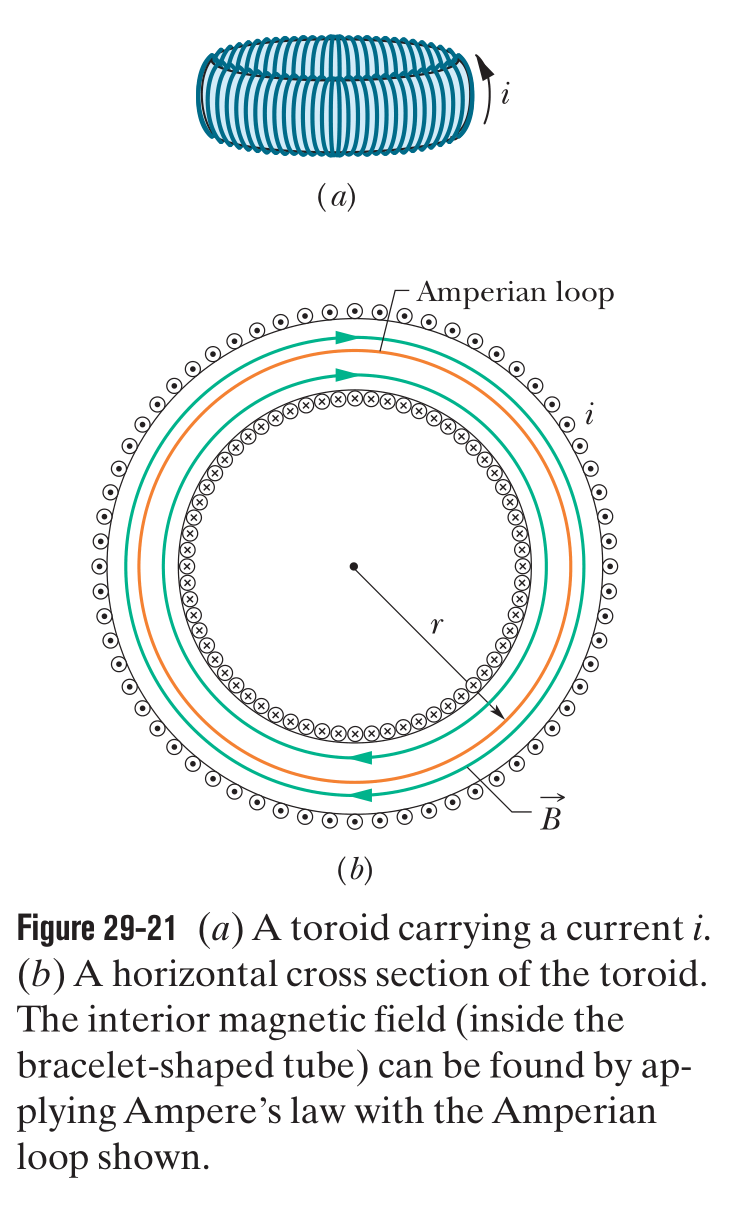
Toroids

A toroid is a hollow solenoid that has been curved until its two ends meet, forming a sort of hollow bracelet. Ampere’s law and the symmetry of the bracelet can be used to calculate the magnetic field $\vec B$ within the toroid.

At a point inside a toroid, the magnitude $B$ of the magnetic field is:

$$B = \frac{\mu_0 iN}{2\pi} \frac{1}{r} \hspace{1em} \textrm{(toroid)}$$

where $r$ is the distance from the center of the toroid to the point.

29.5 - A Current-Carrying Coil as a Magnetic Dipole

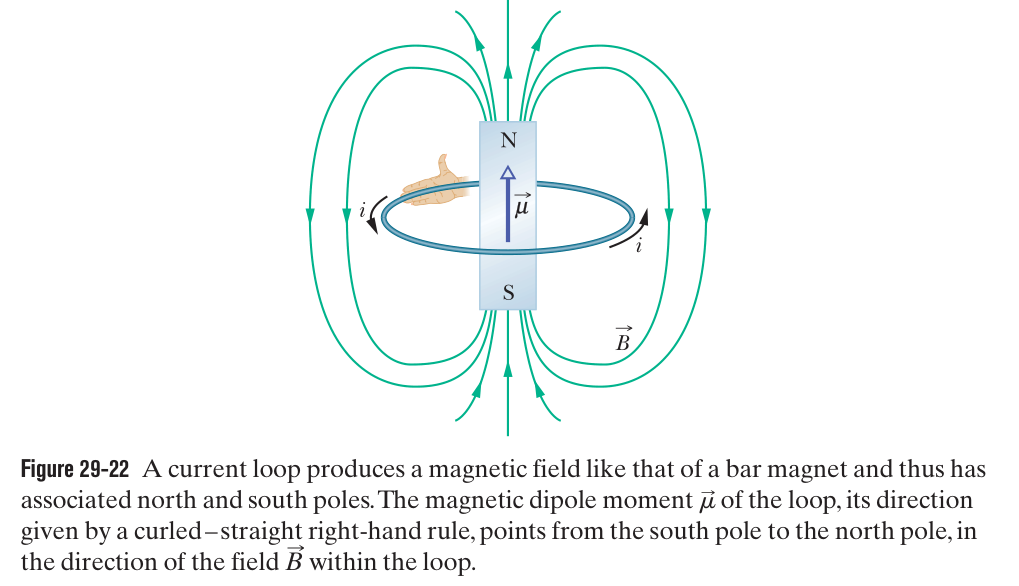
The magnetic field produced by a current-carrying coil, which is a magnetic dipole, at a point $P$ located a distance $z$ along the coil’s perpendicular central axis is parallel to the axis and is given by:

where $\vec \mu$ is the dipole moment of the coil. This equation only applies when $z$ is much greater than the dimensions of the coil.