Unit 23: Gauss’ Law

23.1 - Electric Flux

💡

Key Idea The electric flux

\Phi

through a surface is the amount of electric field that pierces the surface.

The area vector $\vec {dA}$ for an area element (patch element) on a surface is a vector that is perpendicular to the element and has a magnitude equal to the area $dA$ of the element.

The electric flux $d\Phi$ through a patch element with area vector $d \vec A$ is given by a dot product:

d\Phi = \vec E \cdot d\vec A

Total Flux

The total flux through a surface is given by:

\Phi = \int \vec E \cdot d\vec A

where the integration is carried out over the surface.

For a uniform flat surface, this can be written as:

\Phi = (E \cos \phi) A

Net Flux

The net flux through a closed surface (which is used in Gauss’ law) is given by:

\Phi = \oint \vec E \cdot d\vec A

23.2 - Gauss’ Law

Gauss’ law relates the net flux $\Phi$ penetrating a closed surface to the net charge $q_{enc}$ enclosed by the surface:

\epsilon_0 \Phi = q_{enc}

Gauss’ law can also be written in terms of the electric field piercing the enclosing Gaussian surface:

\epsilon_0 \oint \vec E \cdot d\vec A = q_{enc}

23.3 - A Charged Isolated Conductor

💡

Key Idea An excess charge on an isolated conductor is located entirely on the outer surface of the conductor.

The internal electric field of a charged, isolated conductor is zero, and the external field (at nearby points) is perpendicular to the surface and has a magnitude that depends on the surface charge density $\sigma$ :

E = \frac{\sigma}{\epsilon_0}

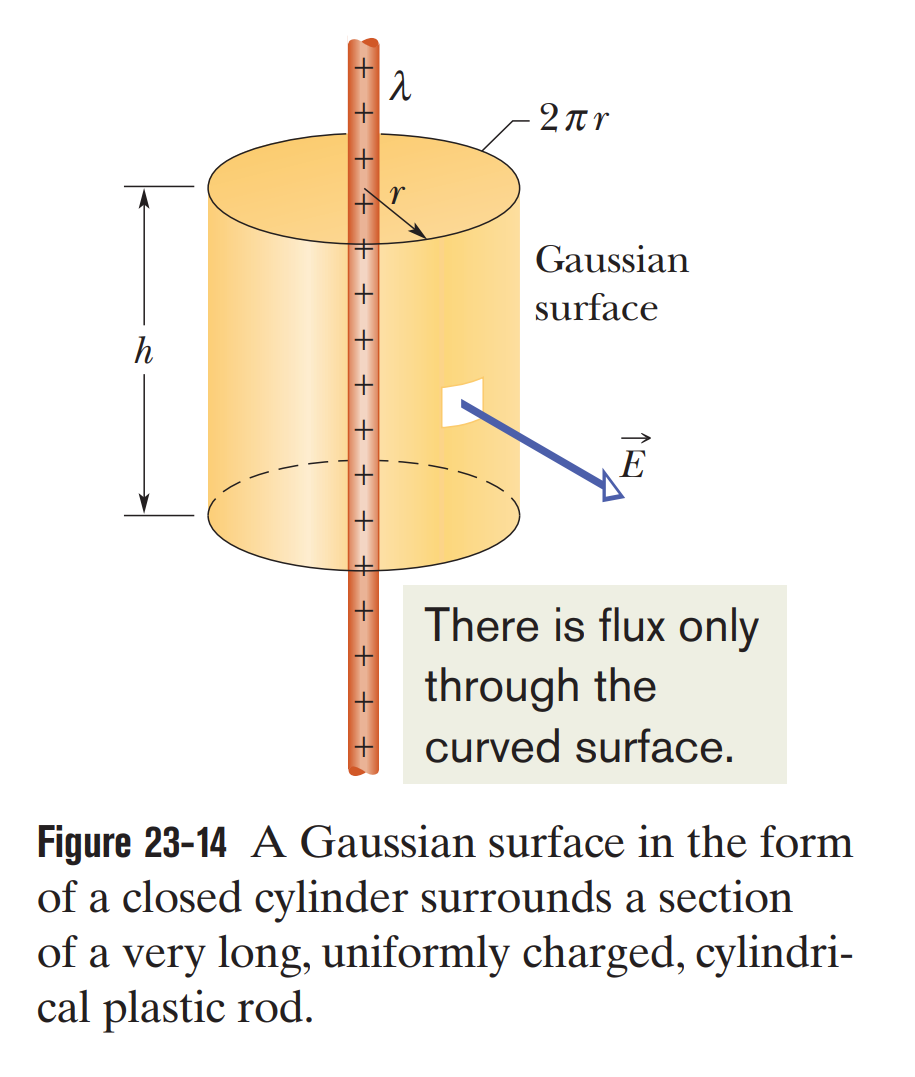
23.4 - Applying Gauss’ Law: Cylindrical Symmetry

The electric field at a point near an infinite line of charge (or charged rod) with uniform linear charge density $\lambda$ is perpendicular to the line and has magnitude:

E = \frac{\lambda}{2\pi \epsilon_0 r}

where $r$ is the perpendicular distance from the line to the point.

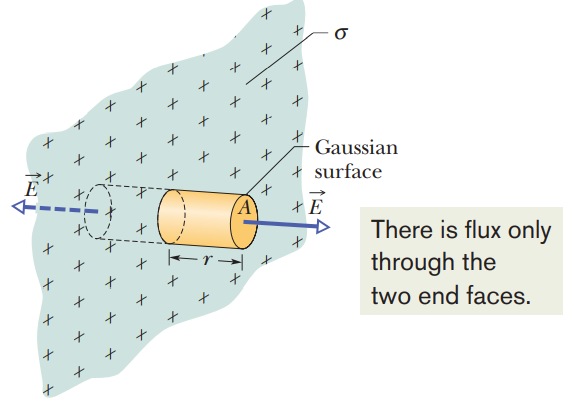
23.5 - Applying Gauss’ Law: Planar Symmetry

Nonconducting Sheet

The electric field due to an infinite nonconducting sheet with uniform surface charge density $\sigma$ is perpendicular to the plane of the sheet and has magnitude:

E = \frac{\sigma}{2\epsilon_0}

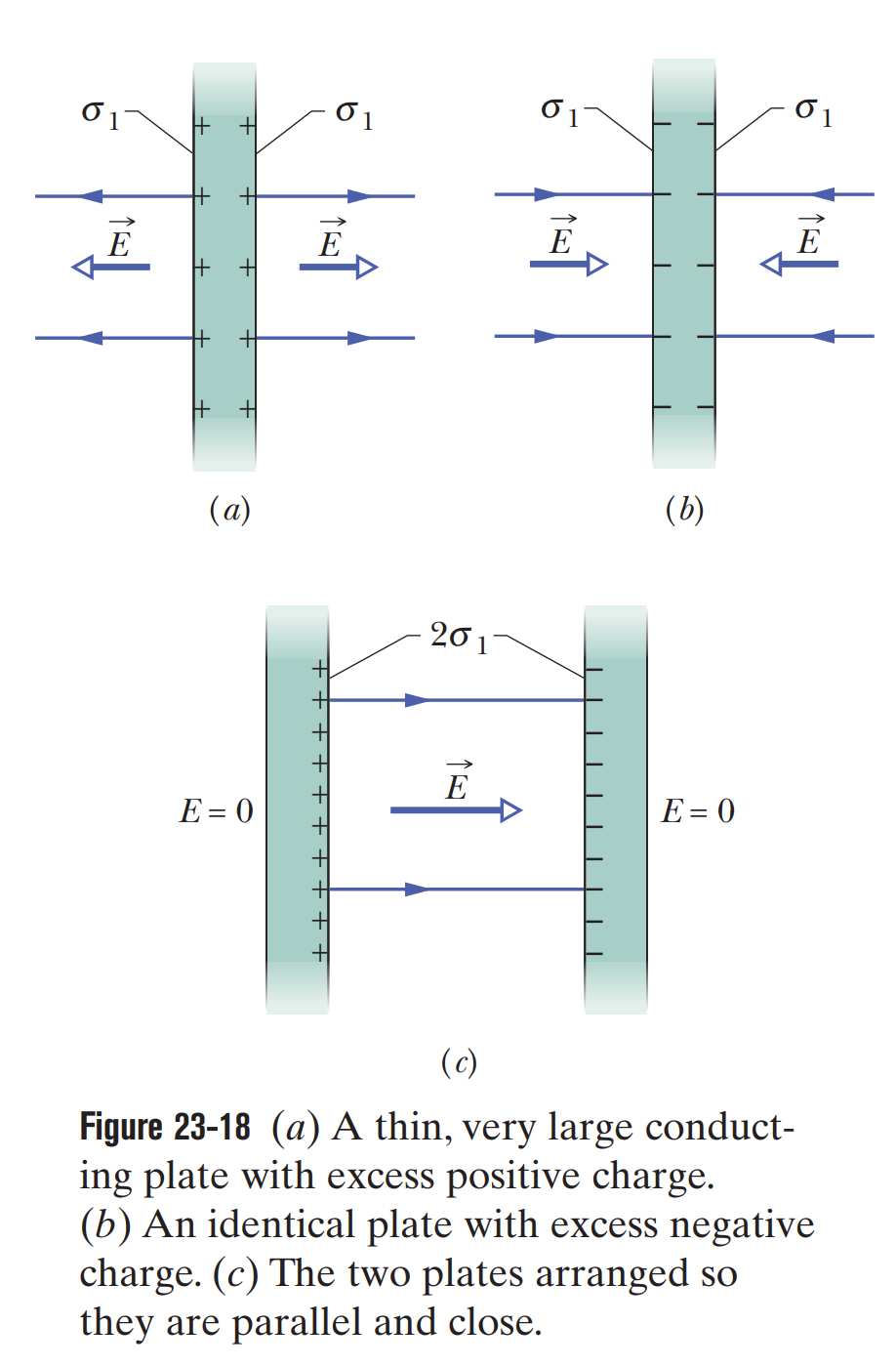
Two Conducting Plates

The external electric field just outside the surface of an isolated charged conductor with surface charge density $\sigma$ is perpendicular to the surface and has magnitude:

E = \frac{\sigma}{\epsilon_0}

Inside the conductor, the electric field is zero.

23.6 - Applying Gauss’ Law: Spherical Symmetry

Spherical Shells

Outside a spherical shell of uniform charge $q$ , the electric field due to the shell is radial (inward or outward, depending on the sign of the charge) and has magnitude:

E = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}

where $r$ is the distance to the point of measurement from the center of the shell. The field is the same as though all of the charge is concentrated as a particle at the center of the shell.

At any point inside the shell, the field due to the shell is zero.

Uniform Spheres

Inside a sphere with a uniform volume charge density, the field is radial and has the magnitude:

E = \frac{1}{4\pi\epsilon_0} \frac{q}{R^3} r

where $q$ is the total charge, $R$ is the sphere’s radius, and $r$ is the radial distance from the center of the sphere to the point of measurement.