15.1 - Simple Harmonic Motion

Important Stuff to Know

• The frequency, $f$, of periodic, or oscillatory, motion is the number of oscillations per second. In SI units, it is measured in hertz: $1 \textrm{ Hz} = 1 \textrm{ s}^{-1}$.

• The period, $T$, is the time required for one complete oscillation, or cycle. It is related to the frequency by $T = 1/f$.

• In simple harmonic motion (SHM), the displacement $x(t)$ of a particle from its equilibrium position is described by the equation:

  $$x = x_m \cos(\omega t + \phi)$$

  in which $x_m$ is the amplitude of the displacement, $\omega t + \phi$ is the phase of the motion, and $\phi$ is the phase constant. The angular frequency $\omega$ is related to the period and the frequency of motion by $\omega = 2 \pi/T = 2\pi f$.

• Differentiating $x(t)$ leads to equations for the particle's SHM velocity and acceleration as functions of time:

  $$v(t) = -\omega x_m \sin(\omega t + \phi)$$

  $$a(t) = -\omega^2 x_m \cos(\omega t + \phi)$$

  $$a(t) = -\omega^2 x(t)$$

  In the velocity function, the positive quantity $\omega x_m$ is the velocity amplitude $v_m$. In the acceleration function, the positive quantity $\omega^2x_m$ is the acceleration magnitude $a_m$.

• A particle with mass $m$ that moves under the influence of a Hooke's law restoring force given by $F = -kx$ is a linear simple harmonic oscillator with:

  $$\omega = \sqrt{\frac{k}{m}} \hspace{1.5em} \small{\textrm{(angular frequency)}}$$

  $$T = 2\pi\sqrt{\frac{m}{k}} \hspace{1.5em} \small{\textrm{(period)}}$$

15.2 - Energy in Simple Harmonic Motion

A particle in simple harmonic motion has, at any time, kinetic energy $K = \frac{1}{2} m v^2$ and potential energy $U = \frac{1}{2} kx^2$. If no friction is present, the mechanical energy $E = K + U$ remains constant even though $K$ and $U$change.

Total Energy

15.3 - An Angular Simple Harmonic Oscillator

A torsion pendulum consists of an object suspended by a wire. When the wire is twisted and released, the object oscillates in angular simple harmonic motion with a period given by:

where $I$ is the rotational inertia of the spinning object about the axis of rotation and $\kappa$ is the torsion constant of the wire.

15.4 - Pendulums, Circular Motion

Simple Pendulum

A simple pendulum consists of a rod of negligible mass that pivots about its upper end, with a particle (the bob) attached at its lower end. If the rod swings through only small angles, its motion is approximately simple harmonic motion with a period given by:

where $I$ is the particle's rotational inertia about the pivot, $m$ is the particle's mass, and $L$ is the rod's length.

Physical Pendulum

A physical pendulum has a more complicated distribution of mass. For small angles of swinging, its motion is simple harmonic motion with a period given by:

where $I$ is the pendulum's rotational inertia about the pivot, $m$ is the pendulum's mass, and $h$ is the distance between the pivot and the pendulum's center of mass.

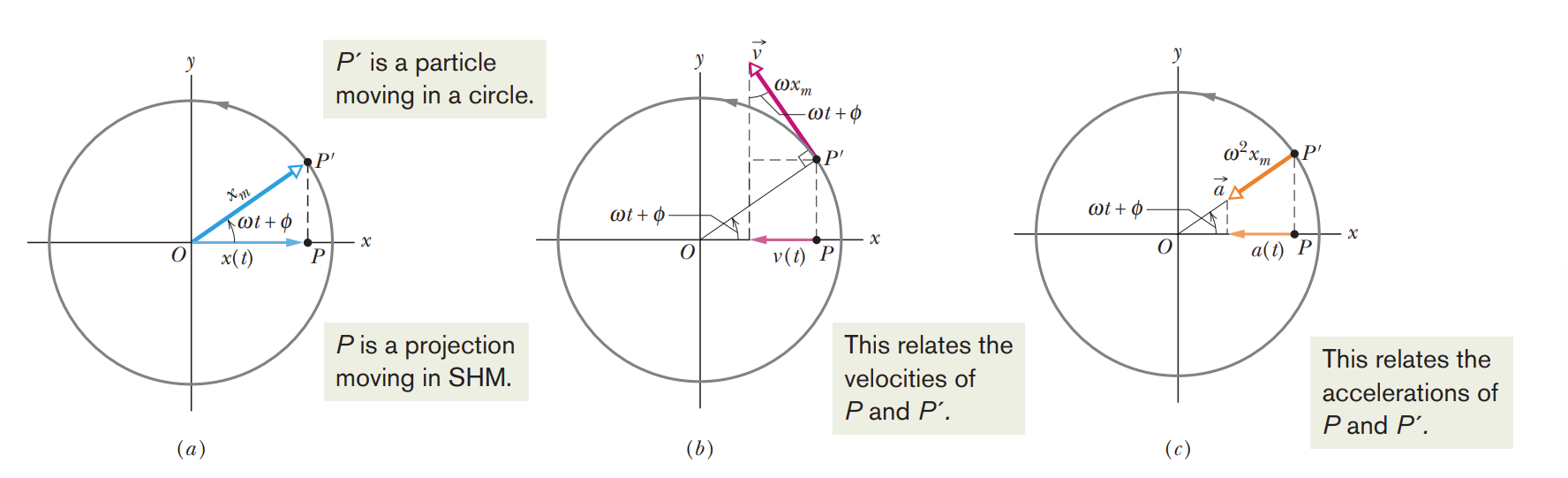
Relating SHM and UCM

Simple harmonic motion corresponds to the projection of uniform circular motion onto a diameter of the circle.

15.5 - Damped Simple Harmonic Motion

The mechanical energy $E$ in a real oscillating system decreases during the oscillations because external forces, such as a drag force, inhibit the oscillations and transfer mechanical energy to thermal energy. The real oscillator and its motion are then said to be damped.

Equations

If the dampening force is given by $\vec F_d = -b\vec v$, where $\vec v$ is the velocity of the oscillator and $b$ is a dampening constant, then the displacement of the oscillator is given by:

where $\omega'$, the angular frequency of the dampened oscillator, is given by:

If the dampening constant is small ($b \ll \sqrt{km}$), then $\omega' \approx \omega$, where $\omega$ is the angular frequency of the undampened oscillator. For a small $b$, the mechanical energy $E$ of the oscillator is given by:

15.6 - Forced Oscillations and Resonance

• If an external driving force with angular frequency $\omega_d$ acts on an oscillating system with natural angular frequency $\omega$, the system oscillates with angular frequency $\omega_d$.

• The velocity amplitude $v_m$ of the system is greatest when $\omega_d = \omega$, a condition called resonance. The amplitude $x_m$ of the system is (approximately) greatest under the same condition.