25.1 - Capacitance

A capacitor consists of two isolated conductors (the plates) with charges $+q$ and $-q$. Its capacitance $C$ is defined from:

where $V$ is the potential difference between the plates.

Therefore,

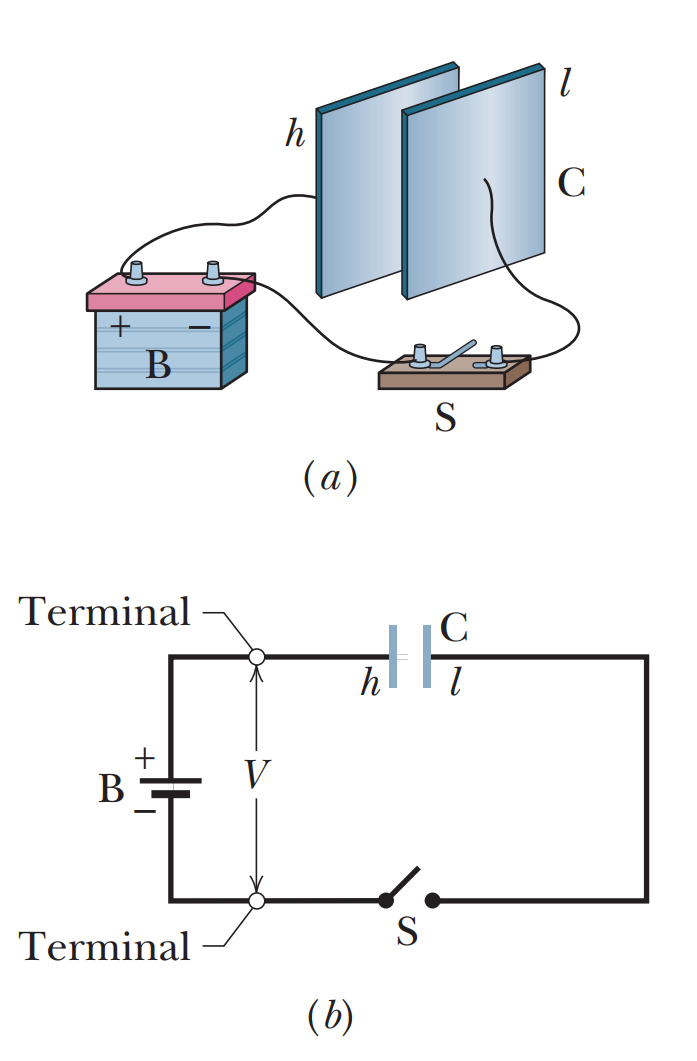
When a circuit with a battery, an open switch, and an uncharged capacitor is completed by closing the switch, conduction electrons shift, leaving the capacitor plates with opposite charges.

25.2 - Calculating the Capacitance

We generally determine the capacitance of a particular capacitor configuration by:

1. Assuming a charge $q$ to have been placed on the plates

2. Finding the electric field due to this charge

3. Evaluating the potential difference $V$ between the plates

4. Calculating $C$ from $q = CV$

Some results are the following:

Parallel-Plate Capacitor

A parallel-plate capacitor with flat parallel plates of area $A$ and spacing $d$ has capacitance:

Cylindrical Capacitor

A cylindrical capacitor (two long coaxial cylinders) of length $L$ and radii $a$ and $b$ has capacitance:

Spherical Capacitor

A spherical capacitor with concentric spherical plates of radii $a$ and $b$ has capacitance:

Isolated Sphere

An isolated sphere of radius $R$ has capacitance:

25.3 - Capacitors in Parallel and in Series

Capacitors in Parallel

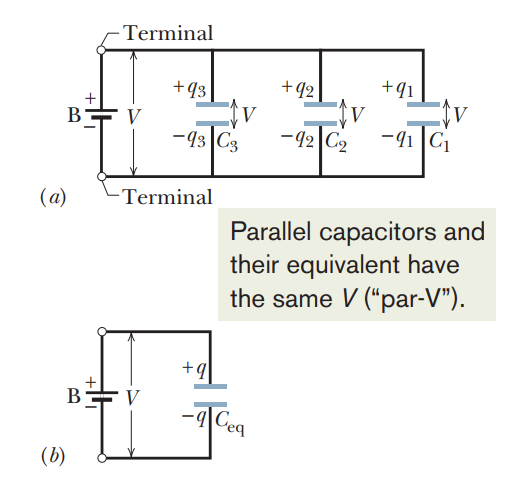
The equivalent capacitance $C_{eq}$ of combinations of individual capacitors connected in parallel can be found from:

Capacitors in parallel share the same voltage, but different currents.

Capacitors in Series

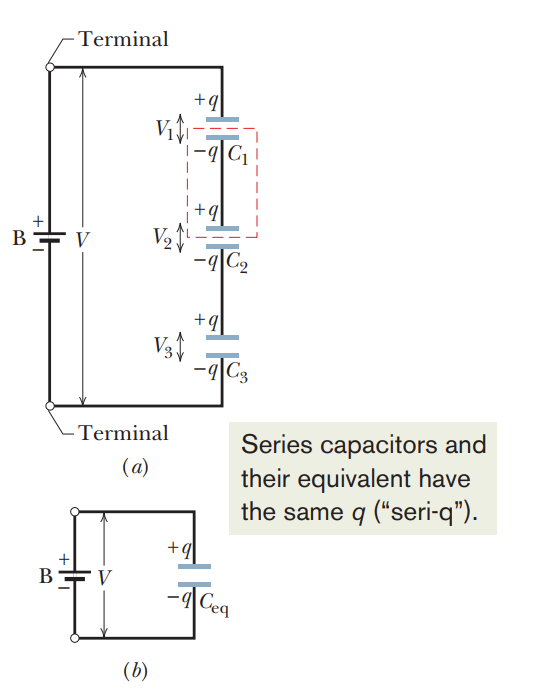
The equivalent capacitance $C_{eq}$ of combinations of individual capacitors connected in series can be found from:

Equivalent capacitances can also be used to calculate the capacitances of more complicated series–parallel combinations.

Capacitors in series have different voltages, but share the same current.

Total capacitance in a series is always less than the smallest individual capacitor.

25.4 - Energy Stored in an Electric Field

The electric potential energy $U$ of a charged capacitor,

is equal to the work required to charge the capacitor. This energy can be associated with the capacitor’s electric field $\vec E$.

Every electric field, in a capacitor or from any other source, has an associated stored energy. In vacuum, the energy density $u$ (potential energy per unit volume) in a field of magnitude $E$ is:

25.5 - Capacitor with a Dielectric

A dielectric is an insulating material such as mineral oil or plastic, which can change the capacitance of a capacitor.

If the space between the plates of a capacitor is completely filled with a dielectric material, the capacitance $C$ in vacuum (or, effectively, in air) is multiplied by the material’s dielectric constant $\kappa$, which is a number greater than 1.

In a region that is completely filled by a dielectric, all electrostatic equations containing the permittivity constant $\epsilon_0$ must be modified by replacing $\epsilon_0$ with $\kappa \epsilon_0$.

When a dielectric material is placed in an external electric field, it develops an internal electric field that is oriented opposite the external field, thus reducing the magnitude of the electric field inside the material.

When a dielectric material is placed in a capacitor with a fixed amount of charge on the surface, the net electric field between the plates is decreased.

25.6 - Dielectrics and Gauss’ Law

Inserting a dielectric into a capacitor causes induced charge to appear on the faces of the dielectric, weakening the electric field between the plates.

The induced charge is less than the free charge on the plates.

When a dielectric is present, Gauss’ law may be generalized to:

where $q$ is the free charge. Any induced surface charge is accounted for by including the dielectric constant $\kappa$ inside the integral.