Unit 24: Electric Potential

24.1 - Electric Potential

The electric potential $V$ at a point $P$ in the electric field of a charged object is:

V = \frac{-W_\infin}{q_0} = \frac{U}{q_0}

where $W_\infin$ is the work that would be done by the electric force on a positive test charge $q_0$ were it brought from an infinite distance to $P$ , and $U$ is the electric potential energy that would then be stored in the test charge-object system.

Electric Potential Energy

If a particle with charge $q$ is placed at a point where the electric potential of a charged object is $V$ , the electric potential energy $U$ of the particle–object system is

U = qV

If the particle moves through a potential difference $\Delta V$ , the change in electric potential energy is

\Delta U = q \Delta V = q(V_f-V_i)

If, instead, an applied force acts on the particle, doing work $W_{app}$ , the change in kinetic energy is

\Delta K = -q\Delta V + W_{app}

In the special case when $\Delta K = 0$ , the work of an applied force involves only the motion of the particle through a potential difference:

W_{app} = q\Delta V

⛔

Warnings to Consider 1.

V

is called a potential, but it should not be confused with potential energy. Yes, the two quantities are related, but they are very different and not interchangeable. 2. Electric potential is a scalar, not a vector.

Language

A potential energy is a property of a system (or configuration) of objects, but sometimes we can get away with assigning it to a single object. For example, the gravitational potential energy of a baseball hit to outfield is actually a potential energy of the baseball–Earth system (because it is associated with the force between the baseball and Earth). However, because only the baseball noticeably moves (its motion does not noticeably affect Earth), we might assign the gravitational potential energy to it alone. In a similar way, if a charged particle is placed in an electric field and has no noticeable effect on the field (or the charged object that sets up the field), we usually assign the electric potential energy to the particle alone.

Units

The SI unit for potential that follows from Eq. 24-2 is the joule per coulomb. This combination occurs so often that a special unit, the volt (abbreviated $V$ ), is used to represent it. Thus,

1 \textrm{ volt} = 1 \textrm{ joule per coulomb}.

With two unit conversions, we can now switch the unit for electric field from newtons per coulomb to a more conventional unit:

1 \textrm{ N/C} = 1 \textrm{ V/m}

From now on, express values of the electric field in volts per meter rather than in newtons per coulomb.

Electron-volts

In atomic and subatomic physics, energy measures in the SI unit of joules often require awkward powers of ten. A more convenient (but non-SI unit) is the electron-volt ( $eV$ ), which is defined to be equal to the work required to move a single elementary charge $e$ (such as that of an electron or proton) through a potential difference $V$ of exactly one volt.

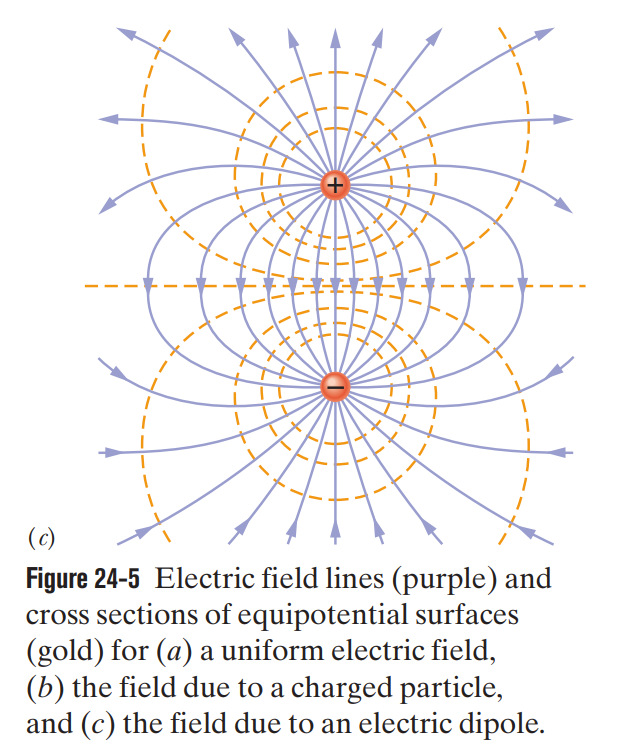
1 \textrm{ eV} = e(1 \textrm{ V}) = (1.602 \times 10^{-19} \textrm{ C})(1 \textrm{ J/C}) \newline = 1.602 \times 10^{-19} \textrm{ J}

24.2 - Equipotential Surfaces and the Electric Field

An equipotential surface is a surface in which every point on the surface has the same electric potential. The work done on a test charge in moving it from one such surface to another is independent of the locations of the initial and final points on these surfaces and of the path that joins the points. The electric field is always directed perpendicularly to corresponding equipotential surfaces.

Electric Potential Difference

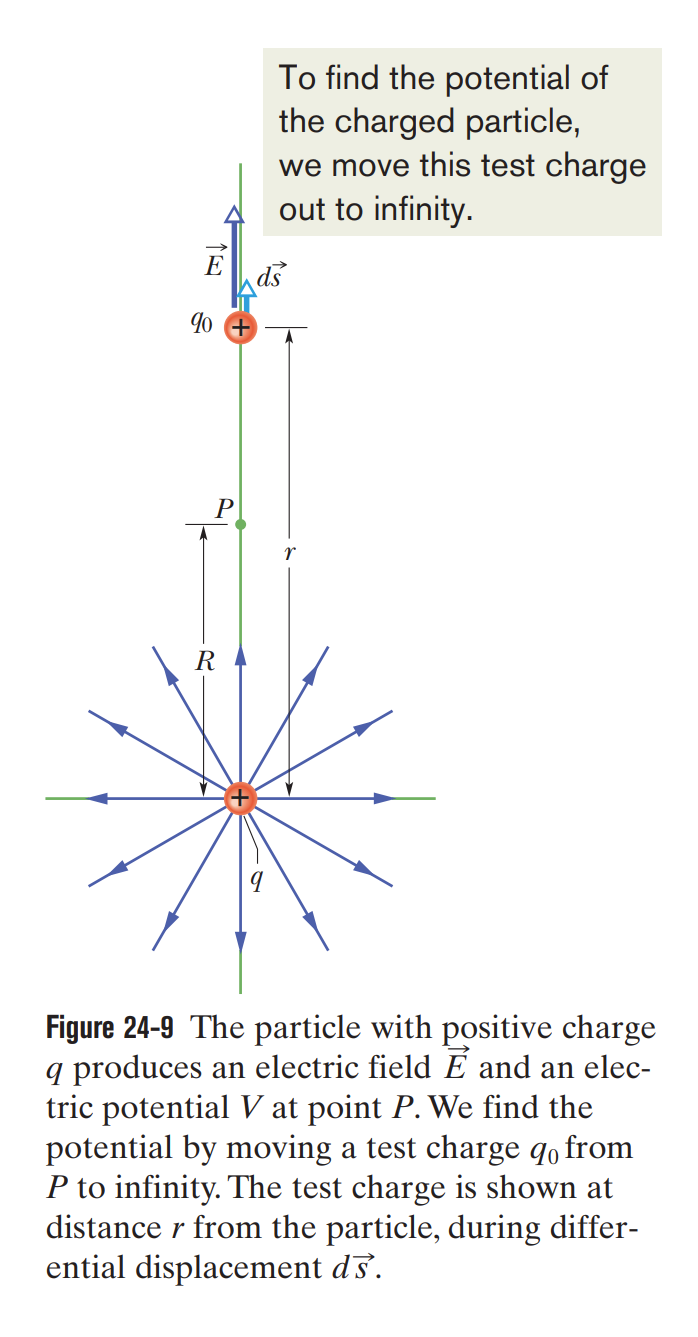
The electric potential difference between two points $i$ and $f$ is

V_f - V_i = -\int_i^f \vec E \cdot d\vec s

where the integral is taken over any path connecting the points. If the integration is difficult along a particular path, we can choose a different path along which the integration might be easier.

If we choose $V_i = 0$ , we have, for the potential at a particular point

V = -\int_i^f \vec E \cdot d \vec s

In a uniform field of magnitude $E$ , the change in potential from a higher equipotential surface to a lower one, separated by distance $\Delta x$ , is

\Delta V = -E \Delta x

24.3 - Potential due to a Charged Particle

The electric potential due to a single charged particle at a distance $r$ from that charged particle is

V = \frac{1}{4\pi\epsilon_0} \frac{q}{r}

where $V$ has the same sign as $q$ .

Collections of Charged Particles

The potential due to a collection of charged particles is

V = \sum_{i = 1}^{n} V_i = \frac{1}{4\pi\epsilon_0} \sum_{i=1}^{n} \frac{q_i}{r_i}

Thus, the potential is the algebraic sum of the individual potentials, with no consideration of directions.

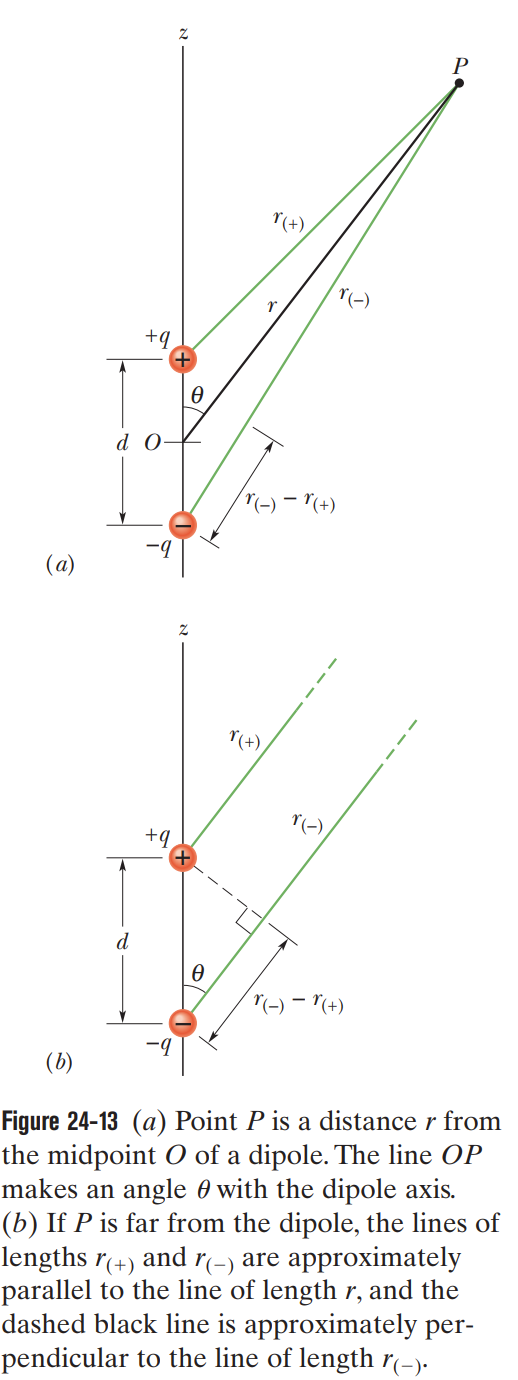
24.4 - Potential due to an Electric Dipole

At a distance $r$ from an electric dipole with dipole moment magnitude $p = qd$ , the electric potential of the dipole is

V = \frac{1}{4\pi\epsilon_0} \frac{p\cos\theta}{r^2}

for $r \gg d$ , the angle $\theta$ lies between the dipole moment vector and a line extending from the dipole moment to the point of measurement.

Induced Dipole Moment

Many molecules, such as water, have permanent electric dipole moments. In other molecules (called nonpolar molecules) and in every isolated atom, the centers of the positive and negative charges coincide (Fig. a) and thus no dipole moment is set up. However, if we place an atom or a nonpolar molecule in an external electric field, the field distorts the electron orbits and separates the centers of positive and negative charge (Fig. b). Because the electrons are negatively charged, they tend to be shifted in a direction opposite the field. This shift sets up a dipole moment that points in the direction of the field. This dipole moment is said to be induced by the field, and the atom or molecule is then said to be polarized by the field (that is, it has a positive side and a negative side). When the field is removed, the induced dipole moment and the polarization disappear.

24.5 - Potential due to a Continuous Charge Distribution

For a continuous distribution of charge (over an extended object), the potential is found by (1) dividing the distribution into charge elements $dq$ that can be treated as particles and then (2) summing the potential due to each element by integrating over the full distribution:

V = \frac{1}{4\pi\epsilon_0} \int \frac{dq}{r}

In order to carry out the integration, $dq$ is replaced with the product of either a linear charge density $\lambda$ and a length element (such as $dx$ ), or a surface charge density $\sigma$ and area element (such as $dx/dy$ ).

In some cases where the charge is symmetrically distributed, a two-dimensional integration can be reduced to a one-dimensional integration.

24.6 - Calculating the Field from the Potential

The component $\vec E$ in any direction is the negative of the rate at which the potential changes with distance in that direction:

E_S = -\frac{\partial V}{\partial s}

The $x$ , $y$ , and $z$ components of $\vec E$ may be found from:

E_x = -\frac{\partial V}{\partial x}

E_y = -\frac{\partial V}{\partial y}

E_z = -\frac{\partial V}{\partial z}

When the electric field $\vec E$ is uniform, this all reduces to:

E = -\frac{\Delta V}{\Delta s}

where $s$ is perpendicular to the equipotential surfaces.

The electric field is zero parallel to an equipotential surface, as the field points directly perpendicular to the surface of the equipotential surface.

24.7 - Electric Potential Energy of a System of Charged Particles

The electric potential energy of a system of charged particles is equal to the work needed to assemble the system with the particles initially at rest and infinitely distant from each other. For two particles at separation $r$ :

U = W = \frac{1}{4\pi \epsilon_0} \frac{q_1q_2}{r}

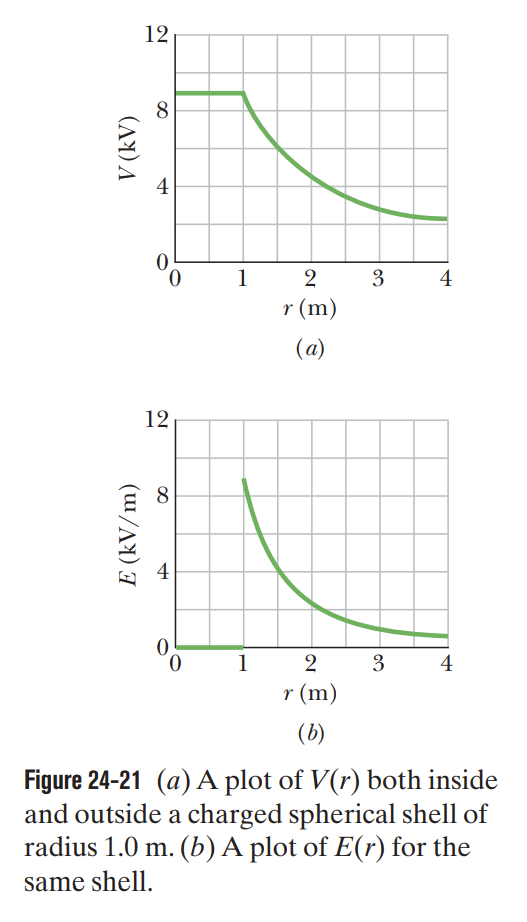
24.8 - Potential of a Charged Isolated Conductor

💡

Key Idea An excess charge placed on a conductor will, in the equilibrium state, be located entirely on the outer surface of the conductor.

The entire conductor, including interior points, is at a uniform potential.

If an isolated charged conductor is placed in an external electric field, then at every internal point, the electric field due to the charge cancels the external electric field that otherwise would have been there.

Also, the net electric field at every point on the surface is perpendicular to the surface.