Unit 22: Electric Fields

22.1 - The Electric Field

A charged particle sets up an electric field (represented as a vector) in the surrounding space. If a second charged particle is located in that space, an electrostatic force acts on it due to the magnitude and direction of the field at its location.

The electric field, $\vec E$ , at any point is defined as the electrostatic force, $\vec F$ , that would be exerted on a positive test charge, $q_0$ , placed there:

\vec E = \frac{\vec F}{q_0}

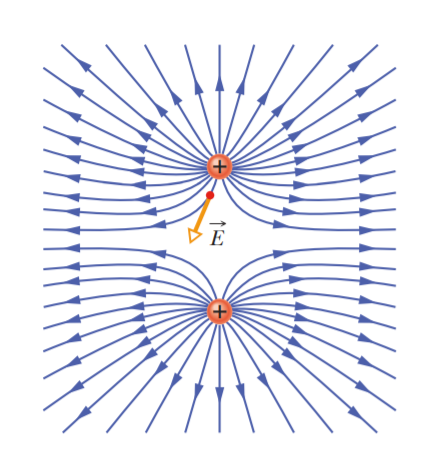
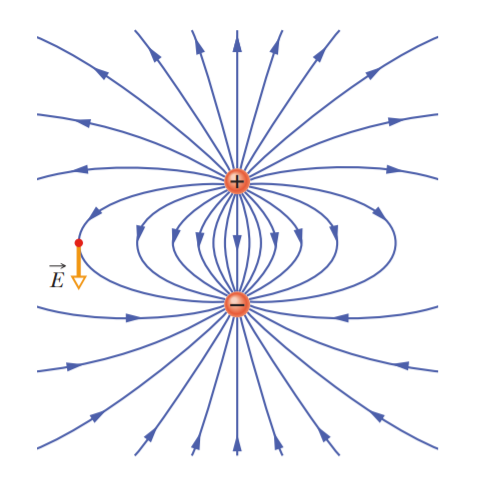
Electric field lines are a way to visualize the direction and magnitude of electric fields. The electric field vector at any point is tangent to the field line through that point. The density of field lines in that region is proportional to the magnitude of the electric field there. Thus, closer field lines represent a stronger field.

Electric field lines originate on positive charges and terminate on negative charges. So, a field line extending from a positive charge must end on a negative charge.

22.2 - The Electric Field Due to a Charged Particle

The magnitude of the electric field $\vec E$ set up by a particle with a charge $q$ at a distance $r$ from the particle is:

E = \frac{1}{4\pi\epsilon_0} \frac{|q|}{r^2}

(this should be familiar)

The electric field vectors set up by a positively charged particle all point directly away from the particle. Those set up by a negatively charged particle all point directly toward the particle.

If more than one charged particle sets up an electric field at a point, the net electric field is the vector sum of the individual electric fields—electric fields obey the superposition principle. (This is how we get repulsion between particles, as shown on the electric field above).

22.3 - The Electric Field Due to a Dipole

An electric dipole consists of two particles with charges of equal magnitude $q$ but opposite signs, separated by a small distance $d$ .

The electric dipole moment $\vec p$ has magnitude $qd$ and points from the negative charge to the positive charge.

The magnitude of the electric field set up by an electric dipole at a distant point on the dipole axis (which runs through both particles) can be written in terms of either the product $qd$ of the magnitude $p$ of the dipole moment:

E = \frac{1}{2\pi\epsilon_0} \frac{qd}{z^3} = \frac{1}{2\pi\epsilon_0} \frac{p}{z^3}

where $z$ is the distance between the pint and the center of the dipole.

Because of the $1/z^3$ dependence, the field magnitude of an electric dipole decreases more rapidly with distance than the field magnitude of either of the individual charges forming the dipole, which depends on $1/r^2$ .

22.4 - The Electric Field Due to a Line of Charge

The equation for the electric field set up by a particle does not apply to an extended object with charge (said to have a continuous charge distribution).

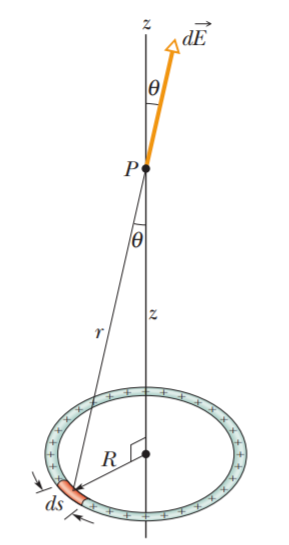
To find the electric field of an extended object at a point, we first consider the electric field set up by a charge element $dq$ in the object, where the element is small enough for us to apply the equation for a particle. Then we sum, via integration, components of the electric fields $d\vec E$ from all the charge elements.

Because the individual electric fields $d\vec E$ have different magnitudes and point in different directions, we first see if symmetry allows us to cancel out any of the components of the fields, to simplify the integration.

By thinking of each little piece as a point charge, $dq$ , the field created by that point charge can be defined as:

d\vec E = k\frac{dq}{d^3}\vec d

where $\vec d$ is the vector from the source (the ring) to the target (point P in the diagram above). The total electric field can then be found through integration:

\vec E = \int d\vec E = \int k\frac{dq}{d^3} \vec d

To make this actually possible to integrate, we need to figure out what $dq$ and $\vec d$ are.

The charge of segment $dq$ is equal to its line charge density $\lambda (x)$  times its length $dL$ , and we can write its length as $dx$  because it lies along the $x$  axis. Therefore

dq = \lambda(x)dx

For $\vec d$ , just use the height and distance given ( $R$ and $z$ in the diagram above) to create a vector pointing upwards from the ring to the point $P$ .

With all this newfound knowledge, here’s what the integral of the diagram above will look like:

\vec E = \int d\vec E = \int_{-L/2}^{L/2} k\frac{\lambda(x)dx}{r^3} (-R \space \hat i + z \space \hat j)

This is the integral of a vector, and you may be wondering how the hell you’re supposed to do that. The answer is “simple”: the unit vectors $\hat i$ , $\hat j$ , and $\hat k$  are all constants: they always point in their respective directions no matter what $x$  is. Therefore, we can pull them out of the integral:

\vec E = -kR\hat i \int_{-L/2}^{L/2} \frac{\lambda(x)dx}{r^3} + kz\hat j \int_{-L/2}^{L/2} \frac{\lambda(x)dx}{r^3}

💡

Tip If the line charge density,

\lambda

, is constant (it usually is in these problems to make your brain hurt less), then you can replace

\lambda(x)

in all the equations above with just the constant

\lambda

, which can then be pulled out of the integrals, leaving just

dx

on top within the integral.

\vec E = -kR\lambda\hat i \int_{-L/2}^{L/2} \frac{dx}{r^3} + kz\lambda\hat j \int_{-L/2}^{L/2} \frac{dx}{r^3}

22.5 - The Electric Field Due to a Charged Disk

On the central axis through a uniformly charged disk,

E = \frac{\sigma}{2\epsilon_0}(1 - \frac{z}{\sqrt{z^2 + R^2}})

gives the electric field magnitude. Here, $z$ is the distance along the axis from the center of the disk, $R$ is the radius of the disk, and $\sigma$ is the surface charge density.

22.6 - A Point Charge in an Electric Field

If a particle with charge $q$ is placed in an external electric field $\vec E$ , an electrostatic force $\vec F$ acts on the particle:

\vec F = q\vec E

If charge $q$ is positive, the force vector is in the same direction as the field vector. If charge $q$ is negative, the force vector is in the opposite direction (the minus sign in the equation reverses the force vector from the field vector).

22.7 - A Dipole in an Electric Field

The torque on an electric dipole of dipole moment $\vec p$ when placed in an external electric field $\vec E$ is given by a cross product:

\tau = \vec p \times \vec E

A potential energy $U$ is associated with the orientation of the dipole moment in the field, as given by a dot product:

U = -\vec p \cdot \vec E

If the dipole orientation changes, the work done by the electric field is:

W = -\Delta U

If the change is due to an external agent, the work done by the agent is:

W_a = -W