Unit 11: Rolling, Torque, and Angular Momentum

11.1 - Rolling as Translation and Rotation Combined

For a wheel of radius $R$ rolling smoothly,

v_{com} = \omega R

where $v_{com}$ is the linear speed of the wheel's center of mass (moving forward), and $\omega$ is the angular speed of the wheel about its center.

Rolling as Pure Rotation

There is another way to look at the rolling motion of a wheel, as pure rotation about an axis which is always at the base of the wheel (where it touches the surface it is rolling on). Rolling motion can be treated as pure rotation passing about that axis, as shown by point $P$ in the diagram to the right.

11.2 - Forces and Kinetic Energy of Rolling

A smoothly rolling wheel has kinetic energy defined as:

K = \frac{1}{2} I_{com} \omega^2 + \frac{1}{2} M v_{com}^2

where $I_{com}$ is the rotational inertia of the wheel about its center of mass and $M$ is the mass of the wheel.

The first term in this equation represents the kinetic energy of the actual rotation of the wheel, while the second term is the linear velocity of the wheel rolling forward.

Linear Acceleration

If the wheel is being accelerated but is still rolling smoothly, the acceleration of the center of mass $\vec a_{com}$ is related to the angular acceleration $\alpha$ about the center with:

a_{com} = \alpha R

Rolling Down a Ramp

If a wheel is rolling smoothly down a ramp of angle $\theta$ , its acceleration along an $x$ axis extending up the ramp is:

a_{com, x} = -\frac{g \sin \theta}{1 + \frac{I_{com}}{MR^2}}

11.3 - The Yo-Yo

A yo-yo, which travels vertically up or down a string, can be treated as a wheel rolling along an inclined plane at angle $\theta = 90\degree$ .

11.4 - Torque Revisited

In three dimensions, torque $\vec \tau$ is a vector quantity defined relative to a fixed point (usually an origin); it is:

\vec \tau = \vec r \times \vec F

where $\vec F$ is a force applied to a particle and $\vec r$ is a position vector locating the particle relative to the fixed point.

11.5 - Angular Momentum

The angular momentum $\vec l$ of a particle with linear momentum $\vec p$ , mass $m$ , and linear velocity $\vec v$ is a vector quantity defined relative to a fixed point (usually an origin) as:

\vec l = \vec r \times \vec p = m(\vec r \times \vec v)

The magnitude of $\vec l$ is given by:

l = rmv \sin \phi

The direction of $\vec l$ is given by the right-hand rule: Position your right hand so that the fingers are in the direction of $\vec r$ .Then rotate them around the palm to be in the direction of $\vec p$ . Your outstretched thumb gives the direction of $\vec l$ .

11.6 - Newton's Law in Angular Form

Newton's Second Law can be written in angular form as:

\vec \tau_{net} = \frac{d \vec l}{dt}

where $\vec \tau_{net}$ is the net torque acting on the particle and $\vec l$ is the angular momentum of the particle.

11.7 - Angular Momentum of a Rigid Body

The angular momentum, $\vec L$ of a system of particles is the vector sum of the angular momenta of the individual particles:

\vec L = \vec l_1 + \vec l_2 + \vec l_3 + \dots + \vec l_n = \sum_{i = 1}^n \vec l_i

Effect of Torque on a System of Particles

The time rate of change of this angular momentum is equal to the net external torque on the system (the vector sum of the torques due to interactions of the particles of the system with particles external to the system):

\vec \tau_{net} = \frac{d\vec L}{dt}

Angular Momentum of a Rigid Body Rotating About a Fixed Axis

For a rigid body rotating about a fixed axis, the component of its angular momentum parallel to the rotation axis is:

L = I\omega

11.8 - Conservation of Angular Momentum

The angular momentum $\vec L$ of a system remains constant if the net external torque acting on the system is zero. Therefore,

\vec L_i = \vec L_f

in an isolated system. This is the law of conservation of angular momentum.

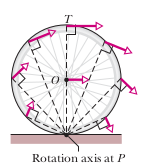
11.9 - Precession of a Gyroscope

A spinning gyroscope can precess about a vertical axis through its support at the rate:

\Omega = \frac{Mgr}{I\omega}

Where $M$ is the gyroscope's mass, $r$ is the moment arm, $I$ is the rotational inertia, and $\omega$ is the spin rate.

Explanation

In this scenario, the torque causing the downward rotation (causing the gyroscope to fall) changes the angular momentum $\vec L$ of the gyroscope, and is caused by the downward force of gravity $M\vec g$ .