Unit 10: Rotation

10.1 - Rotational Variables

To describe the rotation of a rigid body about a fixed axis, called the rotation axis, we assume a reference line is fixed in the body, perpendicular to that axis and rotating with the body. We measure the angular position $\theta$ of this line relative to a fixed direction. When $\theta$ is measured in radians,

\theta = \frac{s}{r}

where $s$ is the arc length of a circular path of radius $r$ and angle $\theta$ .

Radians are related to angular measurements by:

1 \textrm{ rev} = 360\degree = 2 \pi \textrm{ rad}

Angular Displacement

A body that rotates about a rotation axis, changing its angular position from $\theta_1$ to $\theta_2$ , undergoes an angular displacement:

\Delta \theta = \theta_2 - \theta_1

where $\Delta \theta$ is positive for counterclockwise rotation and negative for clockwise rotation.

Angular Velocity

If a body rotates through an angular displacement $\Delta \theta$ in a time interval $\Delta t$ , its average angular velocity $\omega_{avg}$ is:

\omega_{avg} = \frac{\Delta \theta}{\Delta t}

The instantaneous rate of change (angular velocity) can thus be represented as:

\omega = \frac{d\theta}{dt}

Both $\omega_{avg}$ and $\omega$ are vectors, with directions given by a right-hand rule. They are positive for counterclockwise rotation and negative for clockwise rotation. The magnitude of the body’s angular velocity is the angular speed.

Angular Acceleration

If the angular velocity of a body changes from $\omega_1$ to $\omega_2$ in a time interval $\Delta t$ , then the average angular acceleration $\alpha_{avg}$ of the body is

\alpha_{avg} = \frac{\Delta \omega}{\Delta t}

The instantaneous rate of change (angular acceleration) can thus be represented as:

\alpha = \frac{d\omega}{dt}

Both $\alpha_{avg}$ and $\alpha$ are vectors.

10.2 - Constant Angular Acceleration

There are a bunch of kinematic equations for rotational motion, which can all be found here :)

\omega = \omega_0 + \alpha t

\theta - \theta_0 = \omega_0t + \frac{1}{2}\alpha t^2

\omega^2 = \omega_0^2 + 2\alpha (\theta - \theta_0)

\theta - \theta_0 = \frac{1}{2}(\omega_0 + \omega)t

\theta - \theta_0 = \omega t - \frac{1}{2}\alpha t^2

10.3 - Relating the Linear and Angular Variables

Arc Length

A point in a rigid rotating body, at a perpendicular distance $r$ from the rotation axis, moves in a circle with radius $r$ . If the body rotates through an angle $\theta$ , the point moves along an arc with length $s$ given by

s = \theta r

where $\theta$ is in radians.

Linear Velocity

The linear velocity $\vec v$ of the point is tangent to the circle; the point's linear speed $v$ is given by

v = \omega r

where $\omega$ is the angular speed (in radians per second) of the body, and thus also the point.

Linear Acceleration

The linear acceleration $\vec a$ of the point has both tangential and radial components. The tangential component is

a_t = \alpha r

where $\alpha$ is the magnitude of the angular acceleration (in radians per second-squared) of the body. The radial component of $\vec a$ is

a_r = \frac{v^2}{r} = \omega^2r

Period

If the point moves in uniform circular motion, the period $T$ of the motion for the point and the body is

T = \frac{2\pi r}{v} = \frac{2\pi}{\omega}

10.4 - Kinetic Energy of Rotation

Kinetic Energy of Rotation

The kinetic energy $K$ of a rigid body rotating around a fixed axis is given by

K = \frac{1}{2}I\omega^2

in which $I$ is the rotational inertia of the body, defined as

I = \sum m_ir_i^2

for a system of discrete particles.

Rotational Inertia

We call the quantity $I$ the rotational inertia (or moment of inertia) I of the body with respect to the axis of rotation. It is a constant for a particular rigid body and a particular rotation axis.

⛔

The axis of rotation must be specified if the value of

I

is to be meaningful.

10.5 - Calculating the Rotational Inertia

The rotational inertia of a body $I$ can be defined as

I = \sum m_ir_i^2

for a system of discrete particles, or as

I = \int r^2 \space dm

for a body with a continuously distributed mass. The $r$ and $r_i$ in these expressions represent the perpendicular distance from the axis of rotation to each mass element in the body, and the integration is carried out over the entire body so as to include every mass element.

Parallel Axis Theorem

The parallel-axis theorem relates the rotational inertia $I$ of a body about any axis to that of the same body about a parallel axis through the center of mass:

I = I_{com} + Mh^2

Here, $h$ is the perpendicular distance between the two axes, and $I_{com}$ is the rotational inertia about the axis through the com. We can describe $h$ as being the distance the actual rotation axis has been shifted from the rotation axis through the com.

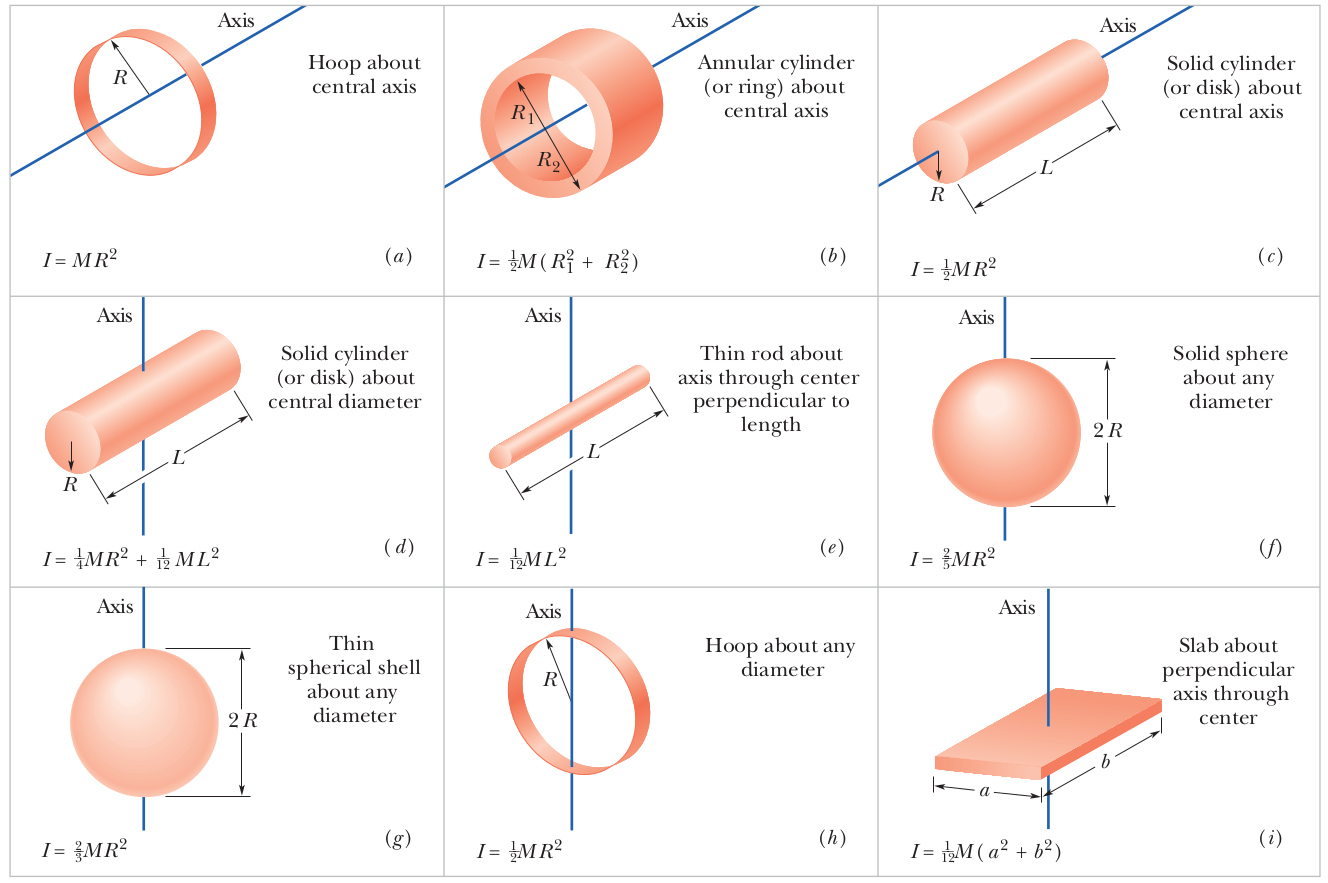
Common Rotational Inertias

10.6 - Torque

Torque is a turning or twisting action on a body about a rotation axis due to a force $\vec F$ . If $\vec F$ is exerted at a point given by the position vector $\vec r$ relative to the axis, then the magnitude of the torque is

\tau = rF_t = r_\perp F = rF \sin \phi

where $F_t$ is the component of $\vec F$ perpendicular to $\vec r$ and $\phi$ is the angle between $\vec r$ and $\vec F$ . The quantity $r_\perp$ is the perpendicular distance between the rotation axis and an extended line running through the $\vec F$ vector. This line is called the line of action of $\vec F$ , and $r_\perp$ is called the moment arm of $\vec F$ . Similarly, $r$ is the moment arm of $F_t$ .

The SI unit of torque is the newton-meter (N*m). A torque $\tau$ is positive if it tends to rotate a body at rest counterclockwise and negative if it tends to rotate the body clockwise.

10.7 - Newton's Second Law for Rotation

The rotational equivalent of Newton's second law is:

\tau_{net} = I\alpha

where $\tau_{net}$ is the net torque acting on a particle or rigid body, $I$ is the rotational inertia of the particle or body about the rotation axis, and $\alpha$ is the resulting angular acceleration about that axis.

10.8 - Work and Rotational Kinetic Energy

The equations used for calculating work and power in rotational motion correspond to equations used for translational motion and are:

W = \int_{\theta_i}^{\theta_f} \tau \space d\theta

P = \frac{dW}{dt} = \tau\omega

Constant Torque

When you have a constant $\tau$ , the integral reduces to:

W = \tau(\theta_f - \theta _i)

Work—Kinetic Energy Theorem for Rotating Bodies

The form of the work-kinetic energy theorem used for rotating bodies is:

\Delta K = K_f - K_i = \frac{1}{2}I\omega_f^2 - \frac{1}{2}I\omega_i^2 = W